Black swans in missing features

A black swan often refers to a rare event, which potentially generates a major impact. Image source
In machine learning, the task is often to predict an outcome based on a set of features. However, it is common that a subset of features are only available in the history (training data), but missing or inaccessible when make a new prediction (testing) for the future. So the question is how to produce a “good” prediction with missing features.
The common ideas are either to learn a model only with the available subset of features, or to learn an additional model for the missing features and then make the prediction based on the imputed features. However, if rare events occur in the missing features, the prediction performance will degrade significantly. In our recent paper [1], we discuss how to make robust predictions when features are missing.
The exploded conditional loss
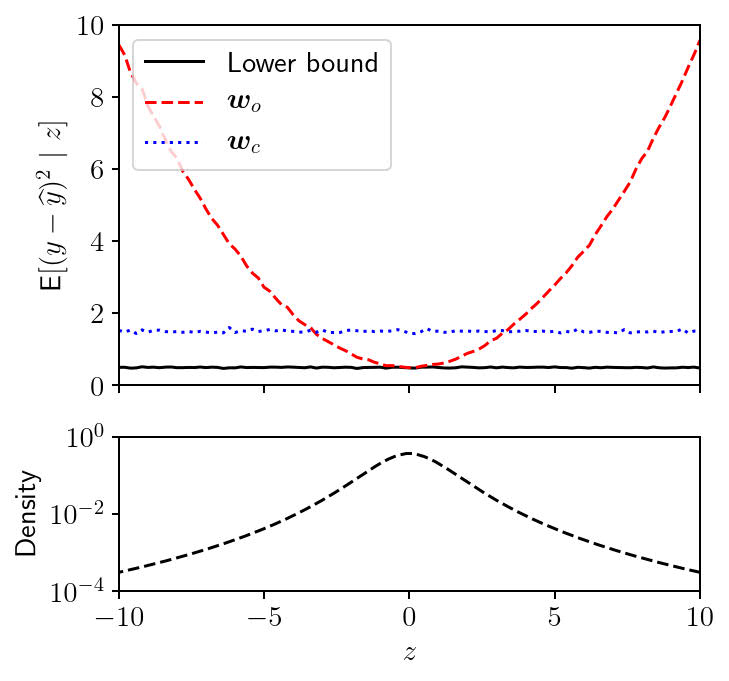
The loss functions given by the optimistic and conservative predictors [1]. Image source
Let \(\begin{bmatrix} \boldsymbol{x}, v \end{bmatrix}\) be the vector of features, and \(z\) is missing. To predict the output \(y\), let’s consider the linear predictor \(\widehat{y} = \boldsymbol{w}^\top \boldsymbol{x}\). The MSE-optimal linear predictor \(\boldsymbol{w}_o\) can be obtained by minimize the following loss function
\[\begin{equation} \boldsymbol{w}_o = \arg\min\ \mathbb{E}[\ (y - \widehat{y})^2\ ] \end{equation},\]where the expectation is with respect to all variables \(\boldsymbol{x}, z, y\). We refer the predictor \(\boldsymbol{w}_o\) as the optimistic predictor. However, if we plot the conditional loss
\[\begin{equation} \mathbb{E}[\ (y - \widehat{y})^2\ |\ z\ ] \end{equation},\]we observe the significantly increased loss when the value of the missing feature \(z\) departs from its mean (the red line). In our paper [1], we showed that this conditional loss has a quadratic growth. We also proofed that the linear imputation of \(z\) will not provide extra information gain.
It is possible to set a constraint that the conditional loss is invariant of \(z\) (the blue line). However, this conservative predictor \(\boldsymbol{w}_c\) will give a significantly increased overall loss, because the typical values of \(z\) will still be around its mean.
Switching bewteen \(\boldsymbol{w}_o\) and \(\boldsymbol{w}_c\)?
Naturally, one will consider a model which switches between \(\boldsymbol{w}_o\) and \(\boldsymbol{w}_c\). The problem is, without observing \(z\) of the testing data, how do we know when to switch between those two predictors?
Our idea is to design a robust predictor which interpolates \(\boldsymbol{w}_o\) and \(\boldsymbol{w}_c\):
\[\begin{equation} \boldsymbol{w} = \text{Pr}\{\ z \text{ in tails}\ |\ \boldsymbol{x}\ \} \boldsymbol{w}_c + \text{Pr}\{\ z \text{ not in tails}\ |\ \boldsymbol{x}\ \} \boldsymbol{w}_o \end{equation},\]where we weight the two predictors using the conditional probability of \(z\) being a rare event, given \(\boldsymbol{x}\). And this conditional probability can be learned from the history, using for example a logistic regression model.
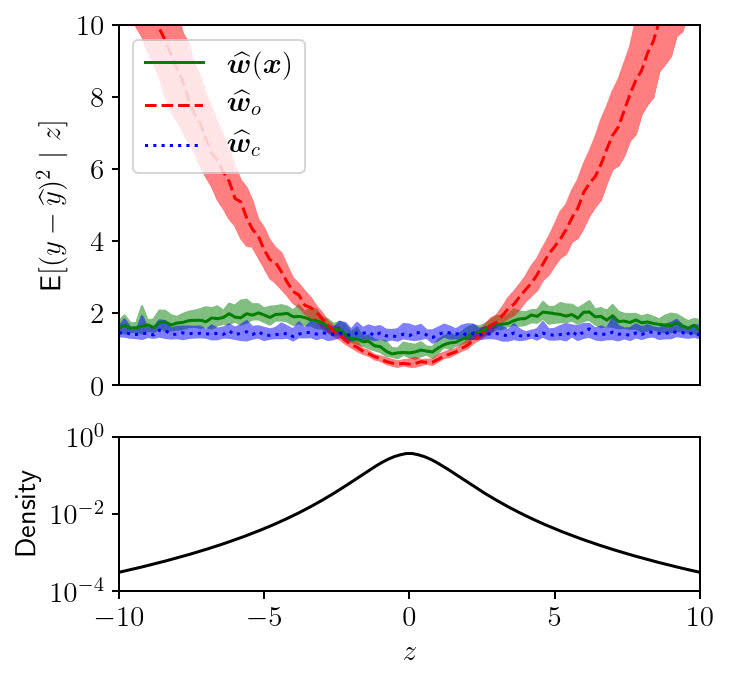
The green line represents the conditional loss given by the robust predictor [1]. Image source
Using the proposed predictor, we are now robust to the “black swans” in the missing feature, without incurring too much error for typical \(z\) values.
References
[1] Liu, Xiuming, Dave Zachariah, and Petre Stoica. “Robust Prediction when Features are Missing.” arXiv preprint arXiv:1912.07226 (2019).